Cuando creas un índice en PostgreSQL, podrías pensar que solo hay un tipo de estructura de índice funcionando entre bastidores. Pero PostgreSQL en realidad proporciona seis tipos diferentes de índices, cada uno diseñado para casos de uso específicos con estructuras internas y patrones de acceso completamente diferentes.
Esta es la parada final en nuestro SQL Query Roadtrip. En el artículo anterior , exploramos cómo el motor de ejecución de PostgreSQL usa el modelo Volcano para transformar planes de consulta abstractos en operaciones concretas. Antes de eso, cubrimos el parsing, análisis, reescritura y planificación. Ahora nos sumergimos en uno de los componentes más críticos que hace todo esto rápido: los índices.
Entender estos tipos de índices no es solo académico—es práctico. Elegir el índice correcto puede transformar una consulta de “timeout después de 30 segundos” a “devuelve resultados en 10 milisegundos”. Vamos a explorar qué hace que cada uno funcione.
La Base Común: La Infraestructura de Índices de PostgreSQL
Antes de sumergirnos en tipos específicos de índices, veamos qué comparten todos. PostgreSQL usa un diseño inteligente: todos los tipos de índices se conectan al mismo framework, como diferentes herramientas que encajan en el mismo mango universal. Esta arquitectura pluggable se llama IndexAmRoutine (definida en src/include/access/amapi.h).
Todos los tipos de índices de PostgreSQL implementan esta misma interfaz, lo que significa que todos necesitan proporcionar funciones para:
- Construir el índice
- Insertar nuevas entradas
- Buscar valores
- Limpiar durante VACUUM
- Estimar costes de consultas
Pero esto es lo que lo hace interesante: mientras comparten esta interfaz, cada tipo de índice tiene estructuras internas completamente diferentes. No solo varían en características de rendimiento—son estructuras de datos fundamentalmente diferentes resolviendo problemas diferentes.
La Arquitectura Slotted Page
Ahora, esta es la base que hace que todos estos índices funcionen: cómo PostgreSQL realmente almacena datos en disco.
Todos los índices comparten el diseño de slotted page de PostgreSQL para almacenamiento. Piensa en cada página de 8KB como una página de cuaderno donde necesitas almacenar elementos de diferentes tamaños. El reto es: ¿cómo los organizas para poder encontrar cosas rápidamente, usar el espacio eficientemente y manejar eliminaciones sin dejar huecos por todas partes?
La solución de PostgreSQL es inteligente. En lugar de solo escribir datos secuencialmente de principio a fin, usa un enfoque de dos lados:
Al frente de la página, hay un array de punteros de línea—esencialmente una tabla de contenidos. Cada puntero es pequeño y de tamaño fijo, diciendo “el elemento #1 comienza en el byte 2047, el elemento #2 comienza en el byte 1998” y así sucesivamente. Este array crece hacia adelante en la página conforme añades más elementos.
Al fondo de la página, los datos reales (tuplas) se almacenan, creciendo hacia atrás hacia el frente. Cada tupla puede tener diferentes tamaños—algunas pequeñas, algunas grandes.
En el medio, tienes espacio libre. Conforme añades elementos, los punteros crecen hacia adelante y los datos crecen hacia atrás, consumiendo este espacio libre. Cuando se encuentran, la página está llena.
Así es como se ve:

Desglosemos lo que estás viendo:
- Sección superior: Cabecera de página (metadata) seguida por el array de punteros de línea creciendo hacia abajo
- Sección media: Espacio libre que se reduce conforme añades más datos
- Sección inferior: Los datos de tupla reales creciendo hacia arriba desde el fondo
- Fondo final: Espacio especial reservado para metadata específica del tipo de índice
¿Por qué este diseño? Porque los punteros son de tamaño fijo y pequeños, puedes hacer búsqueda binaria a través de ellos rápidamente para encontrar un elemento específico. Los datos reales pueden ser de tamaño variable y no necesitan moverse cuando eliminas elementos—solo actualizas el puntero.
También hay un espacio especial al final donde cada tipo de índice almacena su propia metadata personalizada. Para B-trees, esto contiene enlaces de páginas hermanas. Para índices hash, almacena información de buckets. Aquí es donde los diferentes tipos de índices comienzan a divergir en su implementación.
Ahora exploremos cada tipo de índice, empezando con el pilar fundamental de la indexación en PostgreSQL.
B-tree: El Campeón de Propósito General
Cuando creas un índice sin especificar un tipo, PostgreSQL crea un B-tree. Es el predeterminado por una buena razón—es rápido, versátil y maneja la mayoría de casos de uso estupendamente.
Cómo Está Estructurado
Piensa en un B-tree como una jerarquía corporativa. En la cima, tienes ejecutivos (la raíz) que delegan a gerentes (páginas internas), que delegan a trabajadores individuales (páginas hoja) que hacen el trabajo real. Cuando buscas a alguien, empiezas en la cima y sigues la cadena hacia abajo.
El árbol tiene múltiples niveles organizados así:
Las páginas hoja (nivel 0) están en el fondo. Estas almacenan las entradas de índice reales—cada entrada contiene el valor indexado (como un ID de cliente) y un puntero a donde vive esa fila en la tabla heap. Aquí es donde viven los datos reales.
Las páginas internas están en el medio. No almacenan datos reales—solo señales que dicen “los valores 1-100 están por aquí, los valores 101-200 están por allá”. Cada entrada apunta hacia abajo a una página hija que maneja un rango específico de valores.
La página raíz está en la cima. Es el punto de partida para todas las búsquedas. Podría estar en cualquier nivel—un índice pequeño podría tener la raíz apuntando directamente a páginas hoja, mientras que un índice enorme podría tener varias capas de páginas internas en el medio.
Esto es lo que hace especial al B-tree de PostgreSQL: usa el algoritmo Lehman y Yao, que resuelve un problema complicado—¿cómo dejas que múltiples procesos busquen y modifiquen el árbol simultáneamente sin que todo se detenga por el bloqueo?
La innovación clave es añadir enlaces horizontales entre páginas hermanas. Imagina si cada gerente en nuestra jerarquía corporativa también tuviera una línea directa con el gerente de al lado. Esto permite escaneos de rango eficientes—una vez que encuentras la primera página hoja coincidente, puedes simplemente seguir los enlaces hermanos lateralmente sin volver a subir el árbol. También ayuda a las operaciones concurrentes reduciendo la contención de bloqueos.
Así es como se ve un B-tree de PostgreSQL:
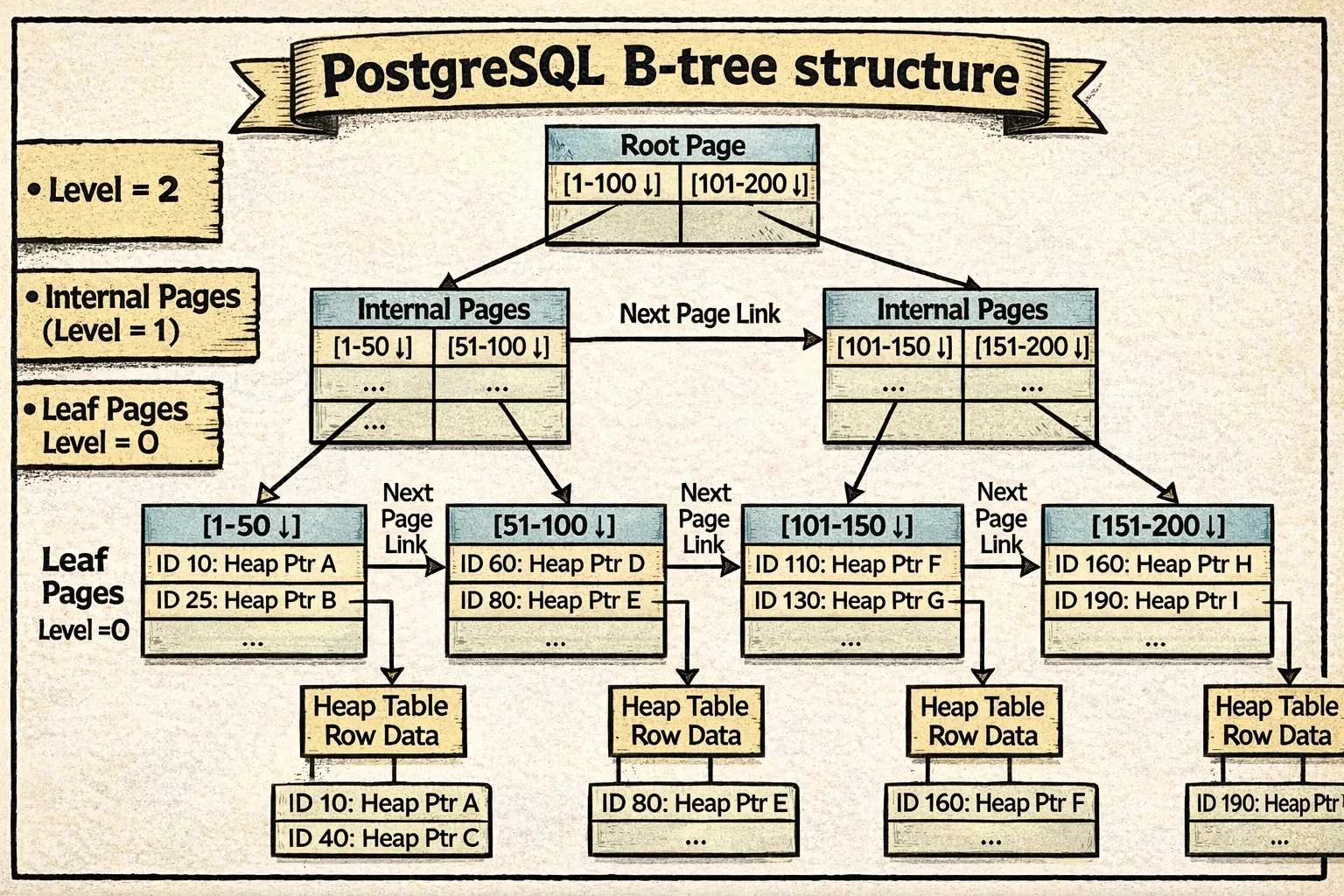
Observa cómo cada nivel forma una cadena horizontal a través de los enlaces hermanos (mostrados como las flechas conectando páginas al mismo nivel). Las flechas verticales muestran relaciones padre-hijo, mientras que los enlaces horizontales permiten escaneos de rango eficientes y acceso concurrente.
Cada página almacena metadata extra en su espacio especial para hacer que esto funcione (ver estructura BTPageOpaqueData). Esta metadata mantiene registro de:
- Punteros hermanos (
btpo_prevybtpo_next) que enlazan cada página a sus vecinos a la izquierda y derecha. Estos crean cadenas horizontales en cada nivel—todas las páginas hoja están enlazadas en una cadena, y todas las páginas internas en cada nivel forman sus propias cadenas. - Nivel del árbol (
btpo_level) que indica qué tan lejos está esta página de las hojas. Las páginas hoja son nivel 0, sus padres son nivel 1, y así sucesivamente. - Flags de página que marcan qué tipo de página es esta (raíz, interna, hoja, eliminada, etc.)
- Cycle ID para detectar divisiones de página concurrentes—un truco inteligente que ayuda a PostgreSQL a saber si la estructura del árbol cambió mientras una búsqueda navegaba hacia abajo.
Con esta estructura en su lugar, veamos cómo PostgreSQL realmente navega y modifica el árbol.
Cómo Funciona el Acceso
Para búsquedas, el descenso en B-tree es notablemente eficiente. Comenzando desde la raíz (que PostgreSQL mantiene en memoria casi todo el tiempo porque se accede con mucha frecuencia), PostgreSQL:
- Lee la página actual
- Si la clave de búsqueda es mayor que la clave alta de la página, sigue el enlace derecho (manejando divisiones concurrentes)
- De lo contrario, hace búsqueda binaria dentro de la página para encontrar el puntero hijo apropiado
- Desciende a ese hijo y repite
Para una tabla con millones de filas, esto típicamente significa 3-4 lecturas de página para alcanzar una hoja, con los niveles superiores en caché en memoria. En la práctica, eso a menudo son solo 1-2 lecturas de disco reales—la diferencia entre 0.1ms (en caché) y 10ms (desde disco) para una consulta.
Para escaneos de rango, una vez que encuentras la primera entrada hoja coincidente, simplemente escaneas hacia adelante (o hacia atrás) a través de páginas hoja usando los enlaces hermanos. No se necesita re-descenso del árbol.
Para inserciones, PostgreSQL desciende a la página hoja apropiada e inserta la nueva tupla. Si la página está llena, divide la página en dos, crea una nueva clave alta e inserta un enlace descendente en el padre (que podría dividirse recursivamente hasta la raíz).
Dada la versatilidad y eficiencia del B-tree, ¿cuándo deberías usarlo versus los tipos de índices especializados?
Cuándo Usarlo
B-tree es tu elección predeterminada. Úsalo para:
- Consultas de igualdad (
WHERE id = 42) - Consultas de rango (
WHERE created_at BETWEEN '2024-01-01' AND '2024-12-31') - Resultados ordenados (
ORDER BY name) - Coincidencias de prefijo (
WHERE name LIKE 'John%') - Restricciones únicas (B-tree es el único índice que soporta
UNIQUE)
La complejidad del B-tree es O(log N) para búsquedas, inserciones y eliminaciones. Para una tabla de mil millones de filas con buena caché, típicamente estás viendo 1-2 lecturas de disco por búsqueda.
La versatilidad del B-tree lo hace la elección predeterminada, pero ¿qué pasa si solo necesitas búsquedas de igualdad y quieres saltarte el recorrido del árbol completamente?
Hash: El Especialista en Igualdad
Si solo necesitas comparaciones de igualdad y quieres búsquedas ligeramente más rápidas, PostgreSQL ofrece índices Hash. Implementan una variante de hashing lineal con encadenamiento de desbordamiento—pero ¿qué significa eso realmente? Vamos a desglosarlo.
📜 Nota histórica: Los índices Hash se consideraban problemáticos en PostgreSQL durante mucho tiempo (no tenían logging WAL hasta PostgreSQL 10, lo que significaba que los crashes podían corromperlos). Ahora son totalmente fiables, pero las mejoras del B-tree a lo largo de los años han reducido la brecha de rendimiento, haciendo que los índices Hash sean relevantes solo en escenarios muy específicos.
Cómo Está Estructurado
Imagina que estás organizando archivos en armarios. En lugar de mantenerlos en orden, usas una regla simple: tomas el número de archivo, haces unas matemáticas con él, y eso te dice en qué cajón ponerlo. Eso es esencialmente cómo funcionan los índices hash.
Los índices hash usan una tabla hash - una estructura donde haces hash de tu valor (como un ID) para obtener un número de bucket, luego buscas en ese bucket. Lo bueno es que encontrar el bucket correcto es matemática instantánea, no búsqueda.
Pero aquí está el reto: ¿qué pasa cuando un bucket se llena? No puedes simplemente redimensionar toda la tabla hash—eso requeriría hacer rehash de todo de una vez, causando pausas masivas.
La solución de PostgreSQL es el hashing lineal, que hace crecer la tabla gradualmente. En lugar de rehacer el hash de todo cuando la tabla se llena demasiado, divide solo un bucket a la vez. Así es como funciona:
- PostgreSQL rastrea un número de bucket “punto de división”
- Cuando el factor de carga general se vuelve muy alto (predeterminado: 75%), divide el bucket en el punto de división
- El punto de división avanza al siguiente bucket
- Esto continúa hasta que todos los buckets en el “nivel” actual han sido divididos, luego comienza de nuevo con un nuevo nivel
Esto mantiene las cosas suaves y predecibles—sin pausas enormes, solo crecimiento gradual.
Pero ¿qué sucede realmente durante una división? Veamos un ejemplo concreto. Digamos que tienes buckets 0-3 (usando 2 bits para determinar bucket: 00, 01, 10, 11), y estás dividiendo el bucket 0:
Antes de la división:
- El bucket 0 contiene todos los valores cuyo hash termina en binario
00(como valores hash 4, 8, 12, 16…) - Los buckets usan 2 bits del hash para determinar la ubicación
Durante la división:
- PostgreSQL crea un nuevo bucket 4
- Re-examina cada entrada en el bucket 0 usando un bit MÁS del hash (3 bits en lugar de 2)
- Las entradas cuyo hash termina en binario
000permanecen en el bucket 0 - Las entradas cuyo hash termina en binario
100se mueven al nuevo bucket 4 - El punto de división avanza al bucket 1 (que será dividido a continuación)
Después de la división:
- El bucket 0 ahora tiene la mitad de sus entradas originales (las que terminan en
000) - El bucket 4 tiene la otra mitad (las que terminan en
100) - Al buscar un valor, PostgreSQL verifica: “¿Este hash corresponde a un número de bucket menor que el punto de división?” Si es sí, usa 3 bits. Si no, usa 2 bits.
Esta es la parte inteligente: la tabla hash crece incrementalmente. No todos los buckets usan el mismo número de bits al mismo tiempo—los buckets que han sido divididos usan un bit más que los buckets que no lo han sido. Cuando todos los buckets han sido divididos, tienes el doble de buckets, todos usan el nuevo conteo de bits, y el ciclo comienza de nuevo en un nuevo nivel.
Ahora veamos cómo PostgreSQL organiza el índice hash en disco. Piensa en ello como un sistema de archivo físico en una oficina con diferentes tipos de almacenamiento:
Metapage (siempre bloque 0) es el centro de control. Abre el archivo de índice hash, y la primera página te dice todo sobre la configuración del índice: cuántos buckets existen actualmente, cuál es el número máximo de bucket, y dónde encontrar cosas. Es como el directorio en la entrada de un edificio—antes de poder navegar a cualquier lugar, lees esto primero.
Páginas de bucket es donde viven los datos reales. Cuando creas un índice hash, PostgreSQL asigna una página primaria para cada bucket. Cuando haces hash de un valor como el ID de cliente 42 y se mapea al bucket 7, esos datos van a la página primaria del bucket 7. Estas son tus ubicaciones de almacenamiento principales.
Páginas de desbordamiento son el mecanismo de expansión. Aquí está el problema: ¿qué pasa si el bucket 7 se vuelve popular y se llena completamente? PostgreSQL crea una página de desbordamiento y la encadena a la página primaria del bucket. ¿Necesitas más espacio? Añade otra página de desbordamiento a la cadena. Es como tener carpetas de archivo expandibles—cuando la carpeta principal se llena, enganchas una carpeta de extensión. Todas estas páginas se enlazan para que puedas recorrer toda la cadena para encontrar lo que necesitas.
Páginas bitmap son el sistema de reciclaje. Cuando eliminas datos del índice hash, las páginas de desbordamiento podrían quedarse vacías. En lugar de solo olvidarse de ellas, PostgreSQL rastrea estas páginas libres en páginas bitmap—esencialmente una lista diciendo “estas páginas de desbordamiento están disponibles para reutilización”. Cuando el bucket 7 necesita una nueva página de desbordamiento, PostgreSQL verifica primero el bitmap antes de asignar una página completamente nueva. Esto evita que el índice crezca para siempre.
Así es como todas estas piezas encajan:
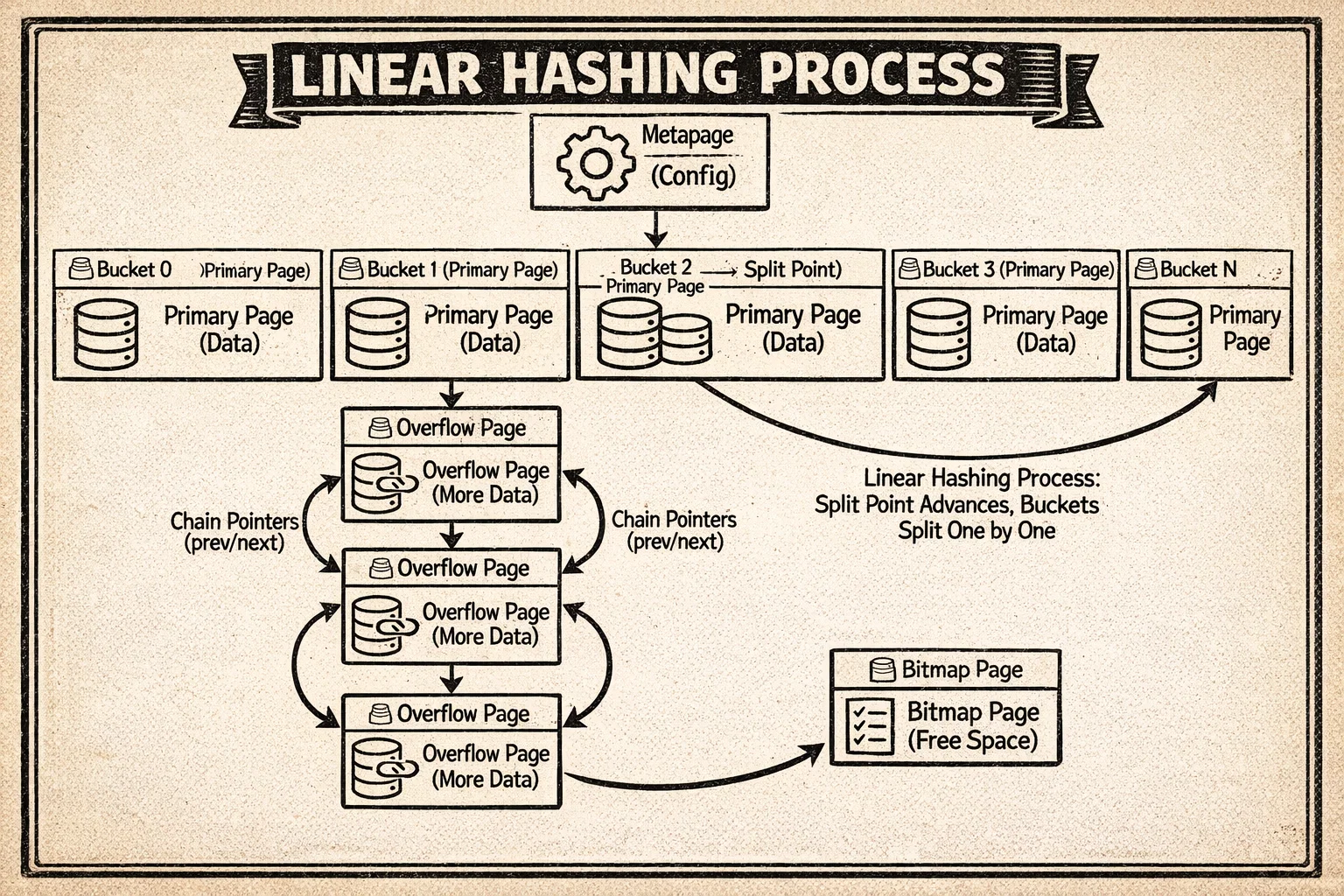
El diagrama muestra la metapage en la cima, las páginas de bucket con su almacenamiento primario, cadenas de desbordamiento extendiéndose desde buckets ocupados, y cómo el proceso de división de hashing lineal redistribuye datos añadiendo nuevos buckets y usando un bit más del valor hash.
Cada página almacena metadata en su espacio especial para mantener estas cadenas (ver estructura HashPageOpaqueData). Esta metadata rastrea:
- Punteros de cadena (
hasho_prevblknoyhasho_nextblkno) que enlazan páginas de desbordamiento. Si un bucket se llena y necesita páginas de desbordamiento, estos punteros crean una cadena doblemente enlazada para que puedas recorrer hacia adelante y hacia atrás a través de todas las páginas pertenecientes a ese bucket. - Número de bucket (
hasho_bucket) que identifica a qué bucket pertenece esta página. Esto es esencial cuando estás recorriendo cadenas de desbordamiento—necesitas saber con qué bucket estás trabajando. - Flags de página que indican qué tipo de página hash es esta (página de bucket primaria, página de desbordamiento, página bitmap, etc.)
La estructura de cadena significa que si el bucket 42 se desborda, puedes seguir los enlaces desde su página primaria a través de todas sus páginas de desbordamiento en secuencia.
Ahora veamos cómo PostgreSQL usa esta estructura hash para manejar inserciones y búsquedas.
Cómo Funciona el Acceso
Para inserciones, PostgreSQL:
- Hace hash de tu valor usando la función hash del tipo (como
hashint4()para enteros) - Mapea el hash de 32 bits a un número de bucket usando enmascaramiento de bits
- Encuentra la página apropiada en la cadena de ese bucket
- Hace búsqueda binaria dentro de la página para mantener orden por valor hash
- Inserta la tupla
Si el factor de carga de la tabla excede el factor de llenado configurado (predeterminado: 75), PostgreSQL dispara una división de bucket: crea un nuevo bucket, rehace el hash de las entradas de un bucket antiguo, y las redistribuye.
Para búsquedas, es similar: hace hash del valor, encuentra el bucket, escanea la cadena del bucket buscando coincidencias. Esto es típicamente O(1) en caso promedio—solo 1-2 lecturas de página para una búsqueda.
Entonces, con toda esta complejidad de hashing lineal y gestión de buckets, ¿cuándo tiene sentido usar Hash sobre B-tree?
Cuándo Usarlo
Los índices Hash son sorprendentemente nicho. La ventaja principal sobre B-tree es evitar el recorrido del árbol—vas directamente a los datos. Pero las limitaciones son severas:
Hash solo es útil para:
- Consultas de igualdad (
WHERE col = value) - Índices de una sola columna
- Columnas de alta cardinalidad
Hash no puede manejar:
- Consultas de rango (
WHERE col > value) - Ordenamiento (
ORDER BY) - Coincidencia de patrones (
LIKE) - Restricciones únicas
- Índices multi-columna
En la práctica, B-tree a menudo es igual de rápido para consultas de igualdad (especialmente cuando los niveles superiores del árbol están en caché) y mucho más versátil. Los índices Hash son una herramienta especializada—útiles cuando tienes una carga de trabajo muy específica solo de igualdad y quieres sacar el máximo rendimiento posible.
Hash maneja bien la igualdad simple, pero ¿qué hay de consultas complejas como “encuentra todos los puntos dentro de esta región” o “qué documentos contienen estas palabras”? Ahí es donde brilla nuestro siguiente tipo de índice.
GiST: El Genio Geométrico
GiST (Generalized Search Tree) no es un solo tipo de índice—es un framework para construir métodos de acceso personalizados. Es particularmente famoso por potenciar PostGIS (bases de datos espaciales), pero maneja mucho más.
Cómo Está Estructurado
Imagina que estás organizando una colección de mapas. En lugar de ordenar los mapas alfabéticamente, los organizas por región: “Mapas de Europa”, “Mapas de Asia”, etc. Pero aquí está la parte complicada—algunos mapas muestran regiones que se superponen (como “Mediterráneo” que incluye partes de Europa, África y Asia). GiST está diseñado para manejar exactamente este tipo de organización superpuesta.
GiST implementa una estructura similar a R-tree que es parecida a B-tree pero con una diferencia crítica: los rangos pueden superponerse. Esto es esencial para datos espaciales como coordenadas geográficas, donde las cajas delimitadoras naturalmente se superponen.
La estructura del árbol se ve familiar:
Las páginas hoja almacenan las entradas de índice reales—cosas como “este polígono” o “este punto”—junto con punteros a donde viven esas filas en la tabla heap.
Las páginas internas no almacenan datos reales. En su lugar, almacenan predicados delimitadores—descripciones de lo que está debajo de ellas. Para datos geométricos, esto podría ser una caja delimitadora: “todo en este subárbol está en algún lugar dentro de este rectángulo”. Para tipos de rango, podría ser “todos los rangos en este subárbol se superponen con este intervalo”.
La página raíz está siempre en el bloque 0, el punto de partida para búsquedas.
La idea clave: a diferencia del B-tree donde sabes exactamente qué hijo seguir (los valores 1-100 van a la izquierda, 101-200 van a la derecha), con GiST podrías necesitar verificar múltiples hijos porque sus predicados delimitadores pueden superponerse. Buscar “puntos cerca del Mediterráneo” podría significar seguir caminos hacia los subárboles de Europa y África.
Así es como se ve un árbol GiST:
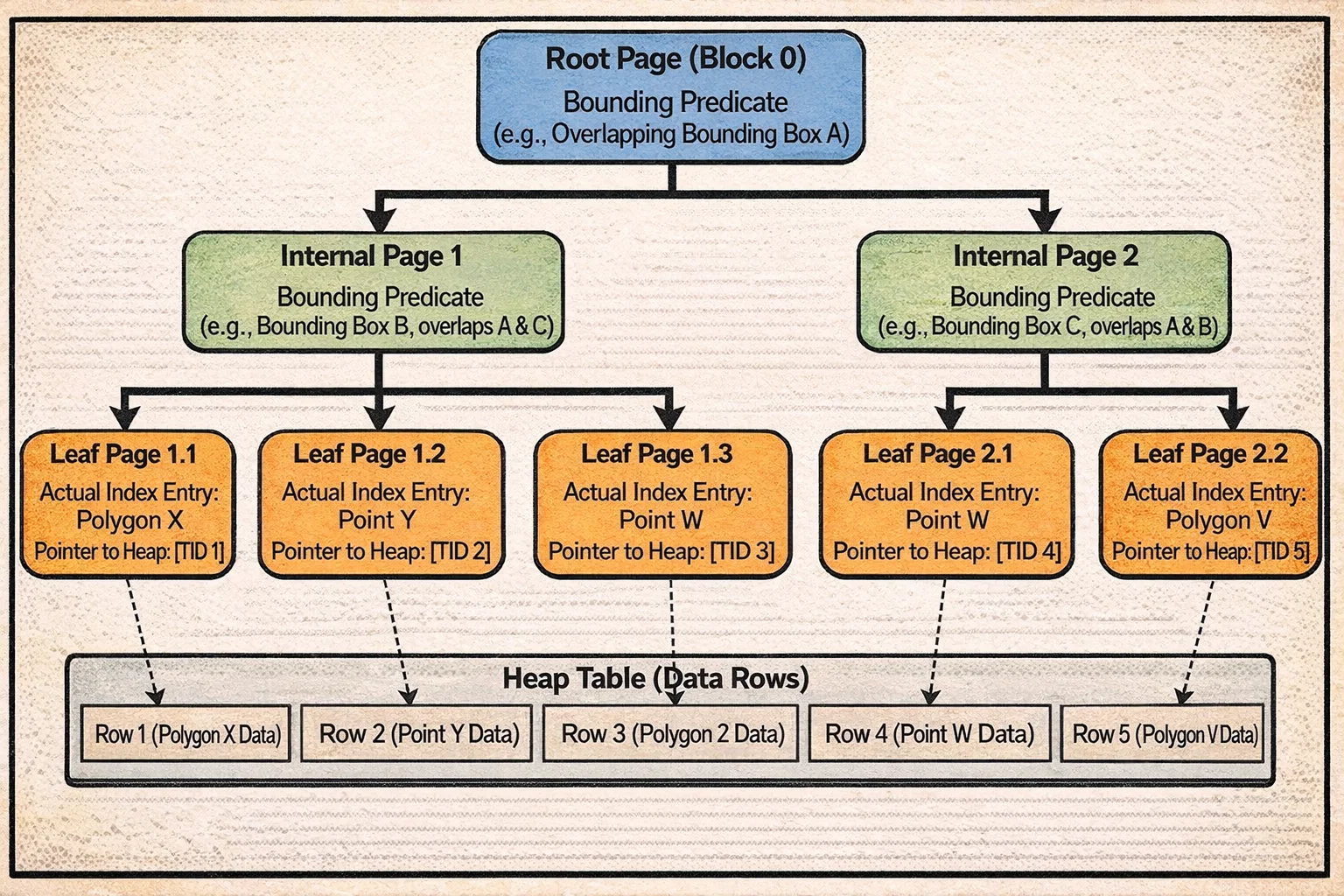
Observa cómo las cajas delimitadoras en el nivel interno pueden superponerse—esta es la diferencia clave con B-tree. Una búsqueda podría necesitar descender a múltiples subárboles porque la región de consulta intersecta con múltiples cajas delimitadoras. Los enlaces derechos entre páginas hermanas (como B-tree) ayudan con el acceso concurrente.
Cada página almacena metadata (ver estructura GISTPageOpaqueData) para manejar el acceso concurrente y la navegación:
- Node Sequence Number (NSN) es un tipo especial de marca de tiempo que se actualiza solo cuando una página se divide. Cuando PostgreSQL está descendiendo el árbol, puede comparar el LSN del padre (log sequence number) con el NSN del hijo. Si el LSN del padre es menor que el NSN del hijo, eso significa que el hijo se dividió mientras la búsqueda estaba en progreso—así que PostgreSQL sabe que necesita seguir el enlace derecho para encontrar todos los datos.
- Enlace derecho apunta a la siguiente página hermana, creando cadenas horizontales igual que B-tree. Esto ayuda con operaciones concurrentes y escaneos de rango.
- Flags de página indican si esta es una página hoja, página interna, o ha sido eliminada.
El NSN es particularmente inteligente—resuelve el problema de detectar divisiones de página concurrentes sin requerir bloqueo costoso durante las búsquedas.
Ahora que entiendes la estructura del árbol GiST, veamos cómo PostgreSQL realmente lo usa para consultas e inserciones.
Cómo Funciona el Acceso
GiST es extensible—diferentes tipos de datos necesitan lógica diferente para organizar datos. Para hacer que esto funcione, cada clase de operador GiST proporciona funciones de soporte que le dicen a PostgreSQL cómo manejar ese tipo específico de datos. Veamos las claves:
Consistent: “¿Este predicado delimitador coincide con mi consulta de búsqueda?” Para datos geométricos, esto podría verificar si una caja delimitadora se superpone con el área de búsqueda.
Union: “Si combino estos predicados, ¿cuál es el predicado delimitador más pequeño que los contiene a todos?” Para datos geométricos, esto crea el rectángulo más pequeño que contiene todos los rectángulos hijos.
Penalty: “Si añado esta nueva entrada a este subárbol, ¿cuánto necesito expandir su predicado delimitador?” Para datos geométricos, esto calcula cuánto más grande necesitaría volverse la caja delimitadora.
PickSplit: “Cuando esta página está llena y necesita dividirse, ¿cómo debo dividir estas entradas en dos grupos?” El objetivo es minimizar la superposición entre los dos grupos resultantes.
Ahora veamos estas funciones en acción.
Para búsquedas, imagina que estás buscando “todos los restaurantes dentro de este barrio” (representado como una caja de búsqueda):
- Comienza en la raíz y verifica la caja delimitadora de cada hijo usando Consistent
- Si una caja delimitadora se superpone con tu área de búsqueda, desciende a ese hijo
- Aquí está la diferencia clave con B-tree: podrías necesitar seguir múltiples hijos porque sus cajas delimitadoras pueden superponerse con tu área de búsqueda
- En el nivel hoja, verifica cada punto/polígono real contra tu consulta
- Devuelve todas las coincidencias
Si tu caja de búsqueda toca tres cajas delimitadoras diferentes en el nivel raíz, seguirás tres caminos hacia abajo del árbol. Con mucha superposición, esto puede volverse costoso.
Para inserciones, digamos que estás añadiendo una nueva ubicación de restaurante:
- Comienza en la raíz y evalúa cada subárbol hijo usando Penalty
- “Si añado este punto a este subárbol, ¿cuánto más grande necesita volverse su caja delimitadora?”
- Elige el hijo con la penalización más pequeña (expansión mínima necesaria)
- Desciende a ese hijo y repite hasta que alcances una hoja
- Inserta la nueva entrada en la página hoja
- Si la página está llena, usa PickSplit para dividir las entradas en dos grupos que minimicen la superposición
- La división podría propagarse hacia arriba del árbol (igual que B-tree)
La calidad de tu función PickSplit marca toda la diferencia. Una buena división crea grupos limpios y no superpuestos. Una mala división crea mucha superposición, lo que significa que las búsquedas tienen que seguir más caminos y el rendimiento se degrada.
Entender la estructura de predicados superpuestos de GiST revela qué problemas resuelve mejor.
Cuándo Usarlo
GiST brilla para:
- Consultas geométricas: Puntos, polígonos, círculos (vía PostGIS)
- Tipos de rango: Verificar si los rangos se superponen o contienen valores
- Direcciones de red: indexación inet/cidr
- Consultas de vecino más cercano:
ORDER BY distance
El rendimiento es O(log N) cuando los predicados están bien separados, pero puede degradarse hacia O(N) si hay alta superposición. La calidad de las funciones Penalty y PickSplit de tu clase de operador marca toda la diferencia.
GiST sobresale en predicados superpuestos para datos espaciales, pero ¿qué hay del escenario opuesto—cuando necesitas encontrar filas que contengan cualquiera de muchos valores posibles, como palabras en un documento o elementos en un array?
GIN: El Maestro del Índice Invertido
GIN (Generalized Inverted Index) voltea el modelo de índice normal de cabeza. En lugar de mapear filas a sus valores, mapea valores a filas. Esto lo hace perfecto para valores compuestos donde cada fila contiene múltiples claves.
Cómo Está Estructurado
Piensa en cómo indexarías un libro. En un índice normal, buscas un número de página para encontrar contenido. Pero ¿qué pasa si quieres buscar por cualquier palabra en el libro? Necesitarías un índice invertido—una lista donde cada palabra apunta a todas las páginas donde aparece. Eso es exactamente lo que hace GIN.
GIN usa una estructura de dos niveles:
Entry Tree (B-tree de claves)
↓
Posting Lists/Trees (ubicaciones de filas para cada clave)
Así es como funciona:
El entry tree es un B-tree que almacena todas las claves únicas que han sido extraídas de tus datos. Para búsqueda de texto completo, estas son palabras. Para una columna de array, estos son los elementos individuales del array. Para JSONB, estos podrían ser claves o valores de los documentos JSON.
Cada entrada en este árbol apunta a una lista de ubicaciones de filas (TIDs - tuple IDs) donde aparece esa clave. Pero aquí es donde se vuelve inteligente: dependiendo de qué tan común es la clave, PostgreSQL usa diferente almacenamiento:
Posting list: Para claves que aparecen en solo unas pocas filas (el umbral actual es alrededor de 384 bytes de datos TID, aproximadamente 64 filas), PostgreSQL almacena un array comprimido simple de TIDs. Es compacto y rápido de escanear.
Posting tree: Para claves que aparecen en muchas filas (como la palabra “the” en un índice de texto completo, que podría aparecer en millones de documentos), una lista simple sería enorme y lenta de buscar. Así que PostgreSQL construye un B-tree separado solo para los TIDs de esa clave. Ahora buscar dentro de esas ubicaciones es eficiente incluso si hay millones.
PostgreSQL convierte automáticamente posting lists a posting trees cuando crecen más allá del umbral. No tienes que pensar en ello—se adapta a tus datos.
También hay una pending list—una estructura separada donde las nuevas entradas de índice se acumulan en modo de actualización rápida antes de ser fusionadas en el índice principal. Esto hace las inserciones masivas mucho más rápidas (exploraremos exactamente cómo en la siguiente sección).
Cada página GIN almacena metadata mínima (ver estructura GinPageOpaqueData)—intencionalmente mantenida pequeña en solo 8 bytes:
- Enlace derecho apunta a la siguiente página, permitiendo que las páginas se encadenen
- Max offset rastrea el número de elementos en la página (el significado varía según el tipo de página)
- Flags de página indican qué tipo de página GIN es esta: página entry tree, página posting tree, página pending list, o metapage
La huella de metadata pequeña es deliberada—las páginas GIN necesitan empacar tantos datos reales como sea posible ya que están almacenando potencialmente millones de entradas posting.
Así es como se ve la estructura GIN:
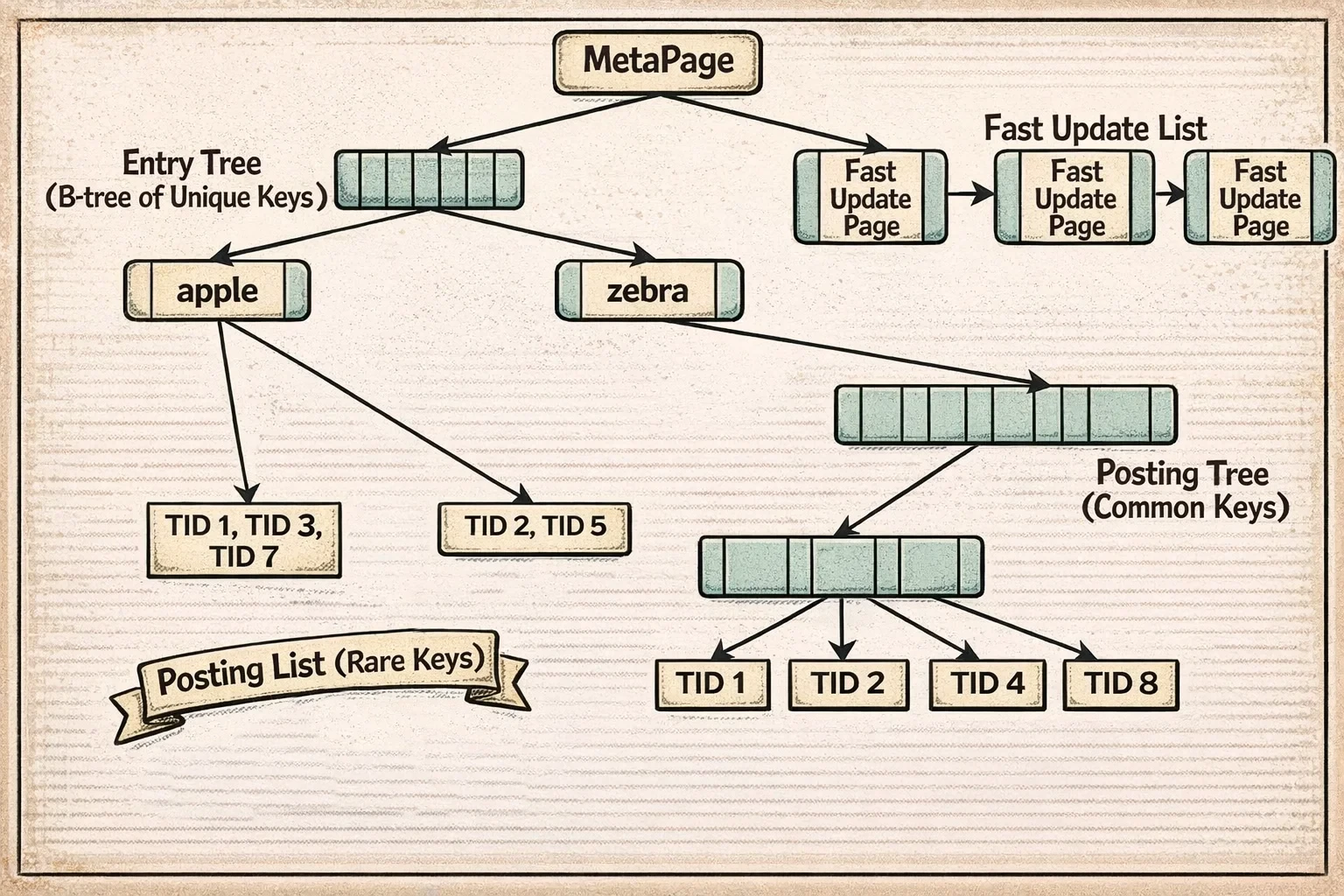
El diagrama muestra el entry tree (un B-tree de claves únicas) en la cima, con cada entrada apuntando a una posting list (para claves poco frecuentes) o un posting tree (para claves comunes). La pending list a un lado acumula nuevas entradas en modo de actualización rápida antes de ser fusionadas en la estructura principal.
Entender esta estructura de dos niveles ayuda a explicar por qué GIN tiene características de rendimiento diferentes para inserciones versus búsquedas.
Cómo Funciona el Acceso
Para inserciones, GIN tiene dos modos:
Modo de actualización rápida (predeterminado): Las nuevas entradas van a una pending list—una lista no ordenada de entradas esperando ser fusionadas. Cuando la pending list se llena (predeterminado: 4MB), se ordena y fusiona en el índice principal en un lote. Esto hace las inserciones masivas 10-100x más rápidas reduciendo el número de modificaciones del árbol.
La contrapartida: las búsquedas tienen que escanear esta pending list no ordenada además de buscar en el índice principal. Para una pending list de 4MB con cientos de miles de entradas, esto podría añadir 10-50ms al tiempo de consulta. Una vez que la pending list se fusiona (lo que sucede automáticamente), las consultas son rápidas de nuevo.
Modo de inserción directa: Cada clave se inserta inmediatamente en el entry tree y su posting list/tree. Más lento para inserciones (porque cada inserción modifica la estructura del árbol principal), pero las búsquedas no pagan la penalización de escanear la pending list.
Para búsquedas:
- Extrae claves de tu consulta (ej., para “postgres & search”, extrae [‘postgres’, ‘search’])
- Busca cada clave en el entry tree (O(log N))
- Recupera la posting list/tree para cada clave (O(log P) + O(P) donde P = coincidencias)
- Combina las listas de TID según la lógica de tu consulta (AND, OR, NOT)
- Escanea la pending list (si usa modo de actualización rápida)
Esta estructura de índice invertido hace de GIN la elección natural para ciertos tipos de consultas.
Cuándo Usarlo
GIN es el índice de referencia para:
- Búsqueda de texto completo: columnas tsvector
- Operaciones de array: operadores
@>,&&,<@ - Consultas JSONB: Existencia de claves, búsquedas de ruta, contención
- Cualquier dato multi-clave: Cada fila contiene múltiples valores a indexar
La eficiencia espacial es notable. Para indexación de texto completo, GIN es típicamente 10-50x más pequeño que crear índices B-tree en todos los términos posibles.
La fortaleza de GIN es manejar valores compuestos con su índice invertido, pero ¿qué pasa si tienes datos que naturalmente se particionan en regiones no superpuestas, como direcciones IP o prefijos de texto?
SP-GiST: El Particionador de Espacio
SP-GiST (Space-Partitioned GiST) está diseñado para estructuras de partición no superpuesta como tries, quad-trees y k-d trees. A diferencia de GiST donde los predicados pueden superponerse, SP-GiST asegura que cada búsqueda siga exactamente un camino a través del árbol.
Cómo Está Estructurado
SP-GiST es en realidad un framework que puede implementar diferentes estructuras de árbol dependiendo de qué estés indexando. Es como tener un sistema de archivo personalizable donde eliges el esquema de organización que mejor se ajusta a tus datos.
El principio clave: en cada nivel del árbol, los datos se particionan en grupos no superpuestos. A diferencia de GiST donde los rangos pueden superponerse (requiriendo múltiples caminos), SP-GiST asegura que siempre hay exactamente un camino a seguir al buscar.
Aquí están las principales estructuras que puede implementar:
Para datos de texto (tries/radix trees):
Imagina organizar palabras descomponiéndolas carácter por carácter. La raíz divide por primera letra (a-z), luego por segunda letra, y así sucesivamente.
- Inner tuples almacenan el prefijo común compartido por todo debajo de ellas, más punteros a hijos etiquetados por el siguiente carácter. Por ejemplo, un nodo podría almacenar “comp” con hijos para “computer” (yendo a ‘u’) y “complete” (yendo a ’l’).
- Leaf tuples almacenan el sufijo restante de la cadena real.
Para puntos 2D (quad-trees):
Piensa en dividir un mapa en cuatro cuadrantes (noroeste, noreste, suroeste, sureste), luego dividir cada cuadrante en cuatro más, y así sucesivamente.
- Inner tuples almacenan un centroide (punto central) y tienen exactamente 4 hijos, uno para cada cuadrante.
- Leaf tuples almacenan los puntos reales.
Para puntos 2D (k-d trees):
Imagina dividir el espacio alternadamente por coordenadas X e Y. El nivel 1 divide por X, el nivel 2 por Y, el nivel 3 por X de nuevo, y así sucesivamente.
- Inner tuples almacenan un valor de coordenada de división y tienen 2 hijos (izquierda/derecha o arriba/abajo dependiendo del nivel).
- Leaf tuples almacenan los puntos reales.
Lo interesante de SP-GiST es que es extensible—puedes implementar esquemas de partición personalizados para tus propios tipos de datos mientras reutilizas el framework central.
Así es como se ve un árbol SP-GiST:
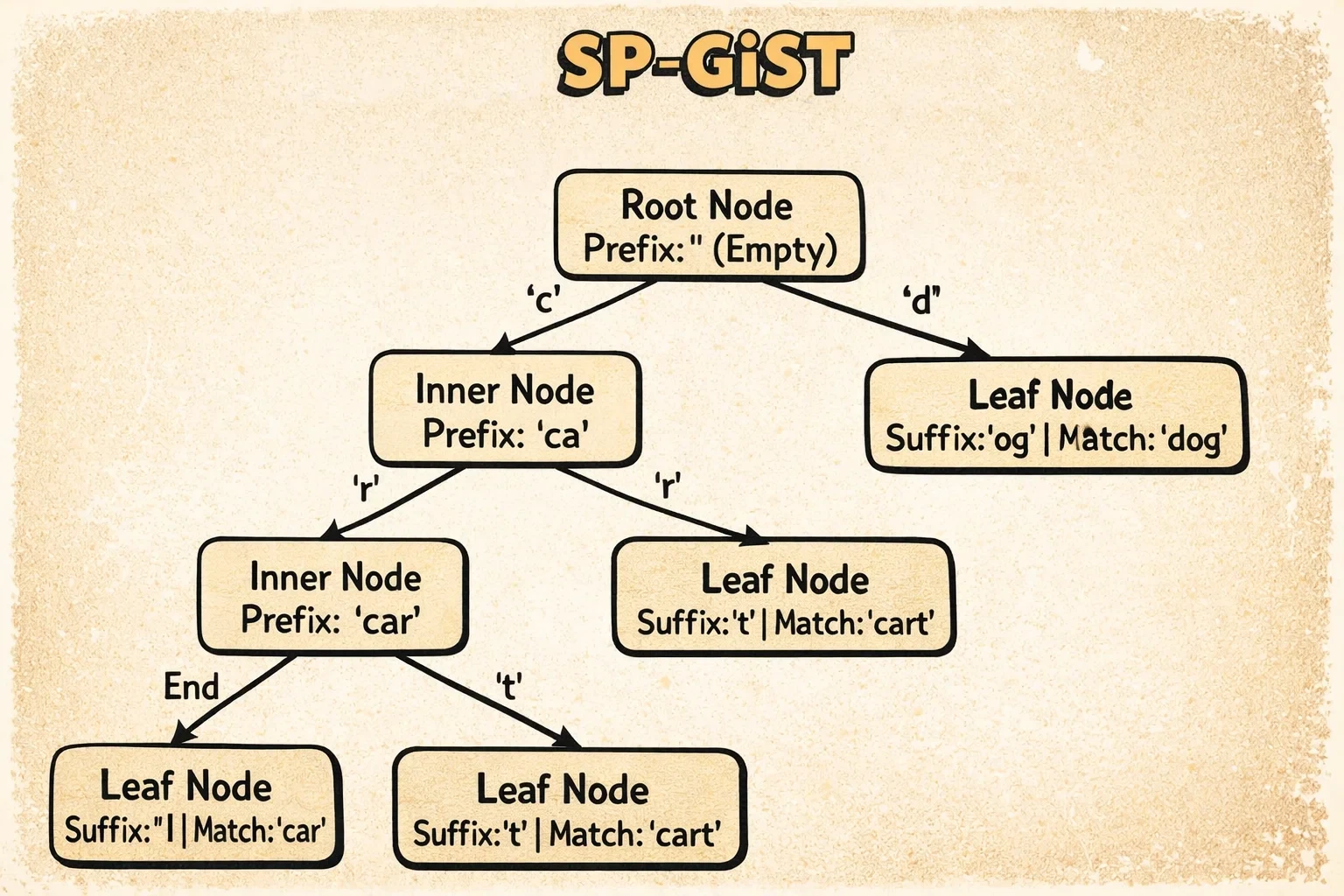
El diagrama muestra cómo SP-GiST implementa un radix tree para texto. Los inner tuples contienen un prefijo (como “comp”) y punteros etiquetados a hijos (como ‘u’ para “computer” o ’l’ para “complete”). Cada búsqueda sigue exactamente un camino a través del árbol basado en el prefijo y las etiquetas—sin regiones superpuestas, sin retroceso.
Cada página SP-GiST almacena metadata (ver estructura SpGistPageOpaqueData) que es única para sus necesidades:
- Flags de página indican qué tipo de página es esta (página inner node, página leaf, página almacenando nulls, o metapage)
- Redirection count rastrea el número de tuplas de redirección en esta página—estos son punteros especiales usados cuando los inner nodes necesitan moverse durante divisiones de página
- Placeholder count cuenta tuplas placeholder, que son marcadores temporales dejados durante operaciones incompletas que necesitan ser limpiadas después
- Page ID es siempre
0xFF82, un número mágico que ayuda a las herramientas a identificar esto como una página SP-GiST
Las tuplas de redirección y placeholder son la forma de SP-GiST de manejar la complejidad de dividir páginas en árboles de partición no superpuestos—es más complicado que las divisiones de B-tree porque no puedes simplemente dividir en cualquier lugar, necesitas mantener la estructura de partición.
La verdadera magia de SP-GiST se vuelve clara cuando ves cómo las búsquedas navegan a través de estas particiones no superpuestas.
Cómo Funciona el Acceso
La idea clave es el descenso de camino único. Al buscar, las funciones de la clase de operador determinan exactamente qué hijo seguir en cada nivel. Sin retroceso, sin múltiples caminos.
Para búsquedas de prefijo de texto usando tries:
- Coincide caracteres de prefijo desde la raíz hasta la hoja
- Sigue exactamente un hijo por nivel basado en el valor del carácter
- La complejidad es O(k) donde k = longitud de cadena (¡independiente del tamaño de la tabla!)
Para búsquedas de puntos usando k-d trees:
- En cada nivel, compara contra la coordenada de división
- Ve a la izquierda o derecha (alternando dimensiones x/y por nivel)
- La complejidad es O(log N) para árboles balanceados
Esta propiedad de descenso de camino único hace de SP-GiST ideal para tipos específicos de datos y consultas.
Cuándo Usarlo
SP-GiST es perfecto para:
- Búsquedas de prefijo de texto:
WHERE name ^@ 'John'(comienza con) - Jerarquías de direcciones IP: rangos inet/cidr
- Consultas de puntos 2D: Usando k-d trees (a menudo más rápido que GiST)
- Cualquier esquema de partición no superpuesta
El radix tree para texto es particularmente elegante—el tiempo de búsqueda depende solo de la longitud de la cadena, no del tamaño de la tabla.
Todos los índices que hemos visto hasta ahora indexan filas o valores individuales. Pero ¿qué pasa si tu tabla es masiva y tus datos tienen ordenamiento natural? Ahí es donde nuestro tipo de índice final toma un enfoque radicalmente diferente.
BRIN: El Índice de Rango de Bloques
BRIN (Block Range Index) es radicalmente diferente de cualquier otro tipo de índice. En lugar de indexar tuplas individuales, almacena información resumida sobre rangos consecutivos de bloques heap.
⚠️ Requisito crítico: BRIN solo funciona bien si tus datos tienen correlación física—lo que significa que el orden en que los valores se almacenan en disco coincide con su orden lógico. Si tienes entradas de log insertadas cronológicamente, los valores de timestamp estarán ordenados físicamente (alta correlación). Si tienes IDs de cliente insertados aleatoriamente, estarán dispersos por la tabla (baja correlación). Volveremos a esto con ejemplos en un momento.
Cómo Está Estructurado
BRIN toma un enfoque radicalmente diferente de otros índices. En lugar de indexar filas individuales, indexa rangos de páginas y almacena información resumida sobre cada rango.
Imagina que tienes un diario que abarca 10 años. En lugar de indexar cada entrada individual, podrías escribir en el lomo de cada cuaderno: “Enero 2020 - Marzo 2020”. Cuando buscas algo de Febrero 2020, sabes exactamente qué cuaderno agarrar. Eso es BRIN.
Así es como funciona:
BRIN divide tu tabla en trozos consecutivos de páginas (predeterminado: 128 páginas por trozo). Para cada trozo, almacena un resumen:
Bloques heap: [0-127] [128-255] [256-383] ...
Rangos BRIN: R0 R1 R2 ...
Resúmenes: [min,max] [min,max] [min,max] ...
Para datos numéricos (clase de operador minmax), cada resumen simplemente almacena los valores mínimo y máximo encontrados en esas 128 páginas. Así que si las páginas 0-127 contienen IDs de cliente que van del 1 al 5000, el resumen almacena [1, 5000].
Para tipos de rango (clase de operador inclusion), almacena la unión de todos los rangos en ese trozo.
Cuando buscas un valor, PostgreSQL escanea a través de estos resúmenes (no los datos reales) y dice “este rango podría contener mi valor, este definitivamente no, este podría…” Luego solo lee los rangos de páginas “podría contener” y verifica cada fila.
El reverse map (revmap) es una tabla de búsqueda que permite a PostgreSQL encontrar rápidamente qué tupla de resumen describe una página dada. Es O(1)—solo acceso directo.
El truco: esto solo funciona bien si tus datos están ordenados físicamente. Si los IDs de cliente 1-5000 están dispersos aleatoriamente por la tabla, cada rango tendrá resumen [1, 5000] y BRIN no proporciona filtrado. Pero si insertas datos en orden (como timestamps), los rangos tienen resúmenes apretados y no superpuestos.
A diferencia de otros tipos de índices, BRIN no usa datos opacos de página estándar. En su lugar, tiene una organización de página única (ver estructura BrinMetaPageData):
- El bloque 0 es una metapage que almacena configuración como cuántas páginas hay en cada rango (
pages_per_range) y dónde está la última página reverse map. También tiene un número mágico (0xA8109CFA) para identificación. - Los bloques subsecuentes son páginas revmap (reverse map) que proporcionan búsqueda O(1) desde cualquier número de bloque heap a su tupla de resumen. Esto es lo que hace que las inserciones y búsquedas BRIN sean tan rápidas—no se necesita recorrido de árbol.
- Los bloques restantes almacenan tuplas de resumen, que son los valores min/max reales (u otro resumen) para cada rango.
Esta estructura es radicalmente más simple que B-tree o GiST—no hay árbol, sin enlaces hermanos, sin navegación compleja. Solo acceso directo a través del revmap.
Así es como BRIN organiza los datos:
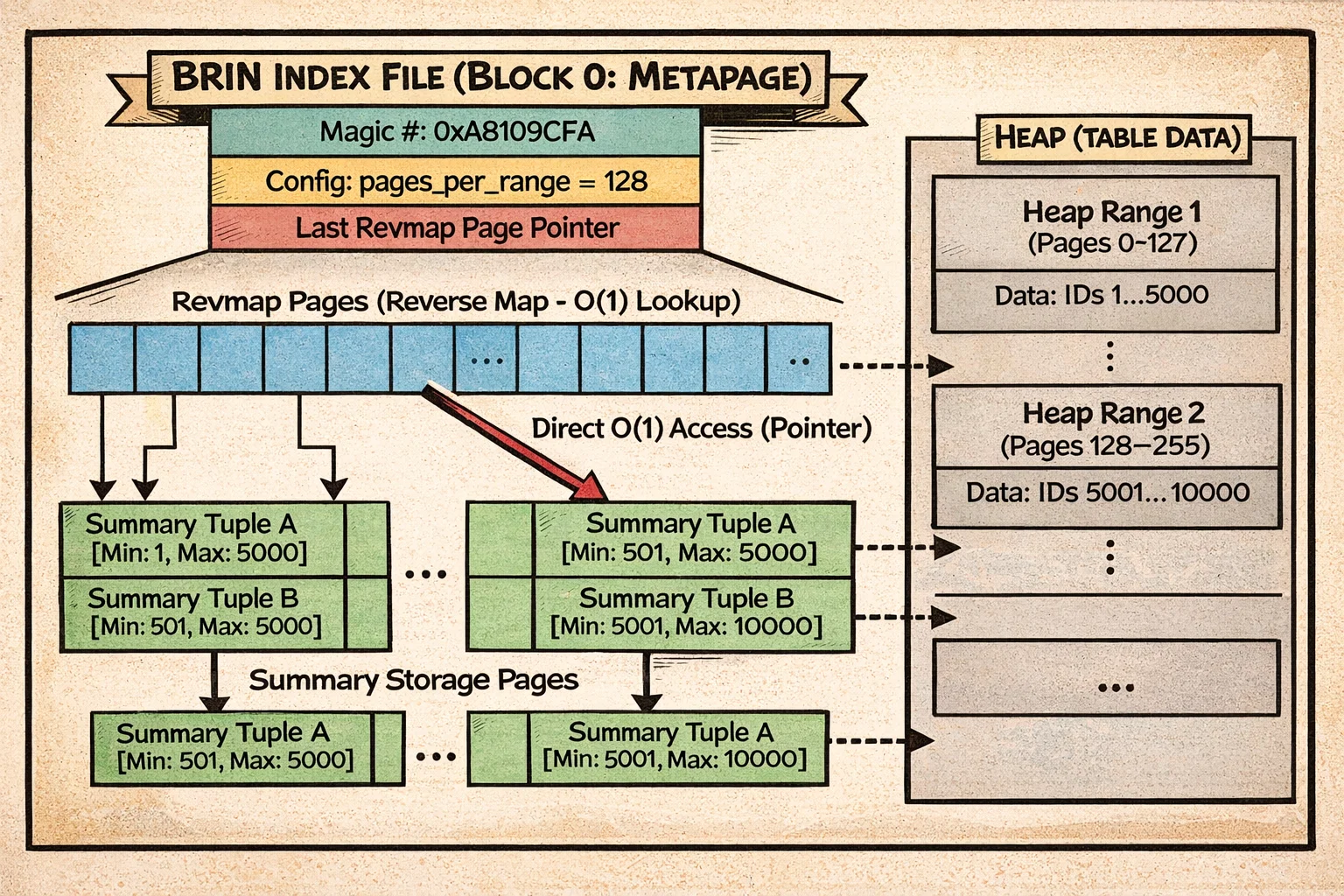
El diagrama muestra la metapage en el bloque 0, seguida por páginas revmap que proporcionan búsqueda O(1) desde rangos de bloques heap a sus tuplas de resumen. Los resúmenes almacenan valores min/max (o filtros bloom, o uniones de rangos) para trozos consecutivos de páginas heap. Observa cómo toda la estructura es plana—sin recorrido de árbol, solo búsqueda directa a través del revmap.
Esta estructura plana simple hace que las operaciones de BRIN sean notablemente directas comparadas con índices basados en árboles.
Cómo Funciona el Acceso
Para inserciones, BRIN es notablemente rápido: O(1). Solo actualiza el min/max para el rango afectado. Sin rebalanceo de árbol, sin estructuras de datos complejas.
Para búsquedas, BRIN escanea todos los resúmenes de rango secuencialmente:
- Lee el revmap
- Para cada rango, verifica si el resumen es consistente con la consulta
- Si es sí, añade el rango completo de 128 páginas a un bitmap
- Devuelve un bitmap con pérdidas (rangos de páginas, no TIDs individuales)
El bitmap heap scan luego lee esos rangos de páginas y reverifica cada tupla.
El Requisito de Correlación
Esta es la idea crítica: BRIN solo funciona bien si tus datos están ordenados físicamente. Si los valores se correlacionan con su ubicación física (correlación > 0.5), BRIN puede excluir la mayoría de los rangos. Si los datos están distribuidos aleatoriamente (correlación cerca de 0), BRIN no proporciona casi ningún filtrado—escanearás toda la tabla.
Caso de uso perfecto: datos de series temporales. Si insertas entradas de log cronológicamente y consultas por timestamp, los resúmenes de BRIN serán apretados. Una consulta por “datos de la última semana” podría coincidir solo con 1-2 rangos de miles.
Con este requisito de correlación en mente, aquí están los escenarios donde BRIN sobresale.
Cuándo Usarlo
BRIN es ideal para:
- Tablas muy grandes (>10GB) con ordenamiento natural
- Datos de series temporales: Timestamps, tablas de logs, sensores IoT
- Cargas de trabajo solo de inserción: Datos insertados en orden
- Consultas de rango en columnas correlacionadas
La eficiencia espacial es impresionante—un índice BRIN puede ser 10,000x más pequeño que B-tree. Para una tabla de 1TB, BRIN podría ser 4MB mientras que B-tree sería 100+GB.
Pero recuerda: verifica la correlación primero usando pg_stats.correlation. Si está por debajo de 0.5, B-tree probablemente sea mejor.
La Matriz de Comparación de Índices
Pongámoslo todo junto. Así es como estos índices se comparan:
Guía de notación:
N= número de filas en la tablaK= número de filas coincidentesP= número de predicados a verificar (para GiST, puede ser > 1 debido a superposición)R= número de rangos de bloques en el índicek= longitud de la clave de búsqueda (para trie SP-GiST)
| Tipo de Índice | Mejor Para | Estructura | Tamaño Típico | Igualdad | Rango | Ordenamiento |
|---|---|---|---|---|---|---|
| B-tree | Propósito general | Árbol balanceado | 10-20% de tabla | O(log N) | O(log N + K) | Sí |
| Hash | Igualdad exacta | Buckets hash | 10-15% de tabla | O(1) | No | No |
| GiST | Espacial, texto completo | Variante R-tree | 15-30% de tabla | O(log N × P) | Sí | Distancia |
| GIN | Arrays, JSONB, texto | Índice invertido | 5-50% de tabla | O(log N + K) | No | No |
| SP-GiST | Tries, particiones | Partición espacial | 10-25% de tabla | O(k) o O(log N) | Limitado | Distancia |
| BRIN | Series temporales | Resúmenes de bloques | 0.001% de tabla | O(R) | O(R) | No |
Concluyendo
Los seis tipos de índices de PostgreSQL no son solo variaciones de rendimiento—son estructuras de datos fundamentalmente diferentes resolviendo problemas diferentes. El árbol balanceado del B-tree maneja consultas generales. La estructura de buckets del Hash optimiza la igualdad. Los predicados superpuestos de GiST permiten consultas espaciales. El índice invertido de GIN hace posible la búsqueda de texto completo. La partición de SP-GiST proporciona descenso de camino único. Los resúmenes de BRIN comprimen gigabytes en megabytes.
Ahora que entiendes cómo funciona cada tipo de índice internamente—sus estructuras, patrones de acceso y trade-offs—estás equipado para explorarlos en tus propias aplicaciones. La mejor manera de interiorizar este conocimiento es experimentar: crea diferentes tipos de índices en tus datos, ejecuta EXPLAIN ANALYZE en tus consultas y mide las diferencias de rendimiento. Lo que funciona mejor depende enteramente de las características específicas de tus datos y patrones de consulta. Un índice GIN podría ser perfecto para un caso de uso mientras que un B-tree sirve mejor a otro, y no hay sustituto para la evaluación práctica con tu carga de trabajo real.
Entender estas estructuras también te ayuda a reconocer cuando algo está mal. Si una consulta con un índice “perfecto” sigue siendo lenta, ahora puedes razonar por qué—tal vez los predicados GiST se están superponiendo mucho, o el supuesto de correlación de BRIN no se cumple para tus datos, o la pending list de GIN ha crecido demasiado. Ya no solo sigues mejores prácticas ciegamente; entiendes los mecanismos detrás de ellas.
¡Y eso concluye nuestro SQL Query Roadtrip! Hemos viajado a través del parsing, análisis, reescritura, planificación, ejecución, y ahora índices. Has visto cómo PostgreSQL transforma tu texto SQL en planes de ejecución optimizados y produce resultados. La próxima vez que ejecutes una consulta, entenderás todo el viaje—desde el momento en que presionas Enter hasta el instante en que los resultados aparecen en tu pantalla.
Los internals son fascinantes, pero recuerda: este conocimiento sirve un propósito. Te ayuda a escribir mejores consultas, diseñar mejores esquemas y depurar problemas de rendimiento con confianza. PostgreSQL está haciendo un trabajo notable entre bastidores, y ahora sabes cómo todo encaja.
